21. Robot Sensing 1

Start Quiz:

Step by Step Walkthrough

The step-by-step breakdown of the solution is pretty quick. Let's recap what's covered in the solution video.

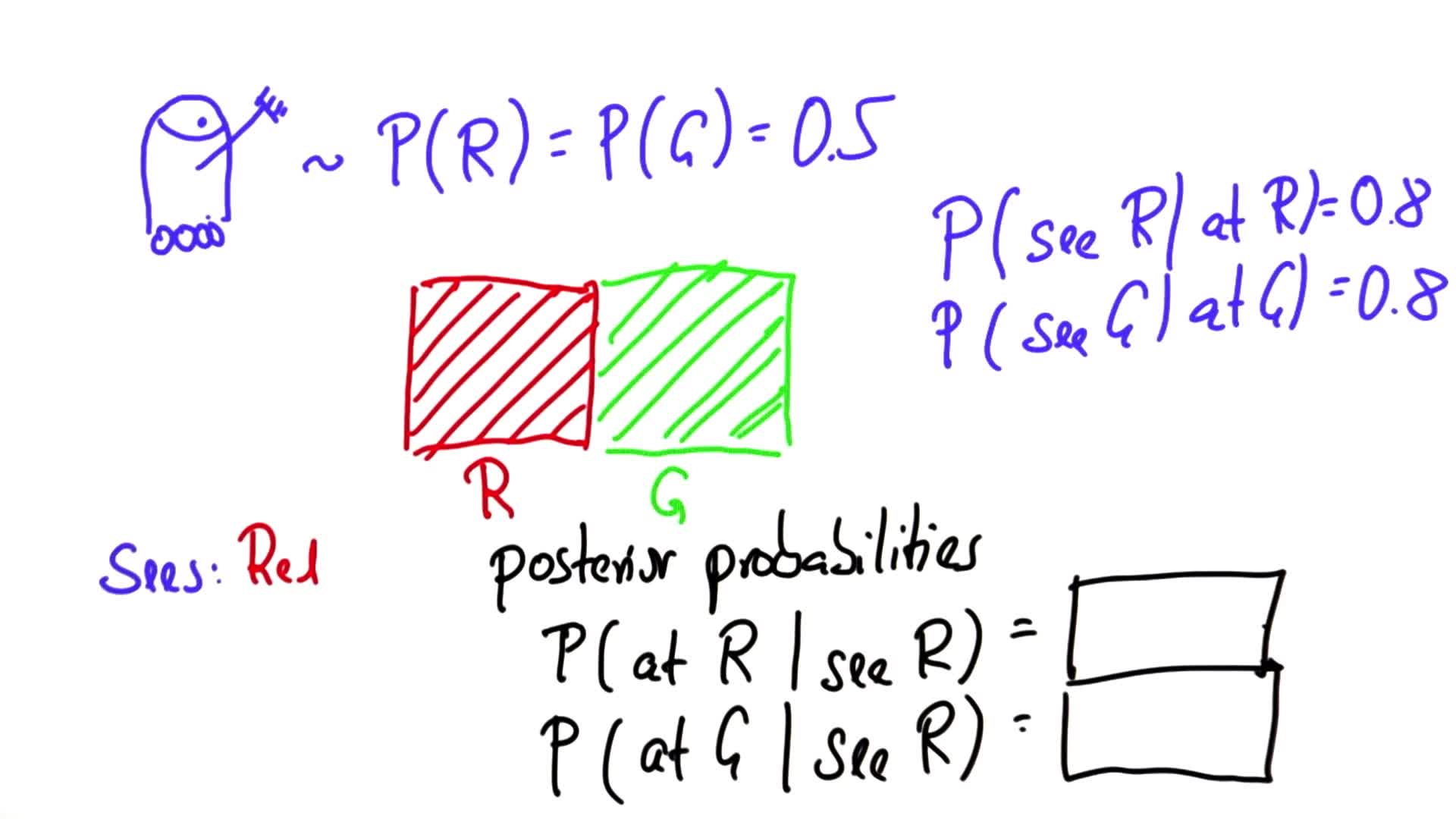
Let's start with what we know:

Prior Probabilities

The robot is perfectly ignorant about where it is, so prior probabilities are as follows:

P(\text{at red} ) = 0.5

P(\text{at green} ) = 0.5

Conditional Probabilities

The robot's sensors are not perfect. Just because the robot sees red does not mean the robot is at red.

P(\text{see red} | \text{at red} ) = 0.8

P(\text{see green} | \text{at green} ) = 0.8

Posterior Probabilities

From these prior and posterior probabilities we are asked to calculate the following posterior probabilities after the robot sees red:

1. P(\text{at red} | \text{see red} )

2. P(\text{at green} | \text{see red} )

and as a reminder, Bayes' rule looks like this:

P(A|B ) = \frac{P(B|A) \cdot P(A)}{P(B)}

or, if we want to use our "versions" of A and B (for posterior #1)…

P(\text{at red}|\text{see red} ) = \frac{P(\text{see red}|\text{at red}) \cdot P(\text{at red})}{P(\text{see red})}

Now, we can read two of those terms from what we already know about our prior and conditional probabilities which means we can rewrite this as…

P(\text{at red}|\text{see red} ) = \frac{0.8 \cdot 0.5}{P(\text{see red})}

But we still have one unknown! What was the probability that we would see red? The answer is 0.5 and there are two ways I can convince myself of that. The first is intuitive and the second is mathematical.

Why is P(see red) 0.5?

Argument 1: Intuitive

Of course it's 0.5! What else could it be? The robot had a 50% belief that it was in red and a 50% belief that it was in green. Sure, its sensors are unreliable but that unreliability is symmetric and not biased towards mistakenly seeing either color.

So whatever the probability of seeing red is, that will also be the probability of seeing green. Since these two colors are the only possible colors the probability MUST be 50% for each!

Argument 2: Mathematical (Law of Total Probability)

There are exactly two situations where the robot would see red.

1. When the robot is in a red square and its sensors work correctly.
2. When the robot is in a green square and its sensors make a mistake.

I just need to add up these two probabilities to get the total probability of seeing red.

P(\text{see red} ) = P(\text{at red}) \cdot P(\text{see red} | \text{at red}) + P(\text{at green}) \cdot P(\text{see red} | \text{at green})

I can read these quantities from above!

P(\text{see red} ) = 0.5 \cdot 0.8 + 0.5 \cdot 0.2

P(\text{see red} ) = 0.4 + 0.1

P(\text{see red} ) = 0.5